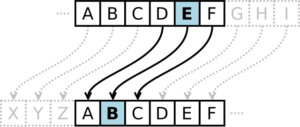
「有名な暗号の問題集」の解答・解説編です
まだ問題を解いてないという方は以下のリンクからご覧ください

なお、問題1, 2の解答・解説は↓に掲載してあります
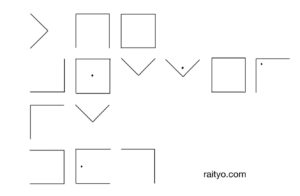
問題3(踊る人形)
問題3:以下の暗号文中の「彼」の名前を答えなさい

この暗号はコナン・ドイルの「踊る人形」に登場する暗号を改題した物です
まず暗号文全体を見てみましょう
普通の英文と違う点に気がつきましたか
そう、単語と単語の間に空白がないのです
このことから、人の持った旗が単語間の空白を表しているのではないかと予想できます
この仮定が正しいとすると、1行目の1文字目と、1行目の6文字目が単独で単語を成していることがわかります
英語で1つのアルファベットで意味をなす単語は I 「私」 と 冠詞の a の2つのみです
そこで以下の2通りのパターンが考えられます
I ?a?? a ???????
?i? ?a?? i? ???
?? i? a? ???i????
or
A ?i?? I ???????
?a? ?i?? a? ???
?? a? i? ???a????
ここで「私」を意味する I が文中に来ることは比較的少ないこと(なくはないですが)から、上のパターンが正しいと仮定して考察していきます
次に、それぞれの文字が出現する回数を数えてみましょう
一番出現する回数が多い文字は1行目の5番目の文字で7回。
次に出現する回数が多いのは
・1行目の1文字目(i か a)
・1行目の2文字目
・1行目の6文字目(i か a)
・2行目の4文字目
の文字で4回ずつ出現します
一般的な英文では「e」の出現頻度が圧倒的に多く、etaoin… の順になるとされています。
さらに英語では2文字連続で並ぶ文字はeやoであることが多いです
そのため後ろから2文字目と3文字目はeeかooとなる確率が高いです
以上の根拠から、最も頻出の文字をeとみなすと以下のようになります
I ?a?e a ?????e?
?i? ?a?e i? ???
?e i? a? e??i?ee?
ここで、問題文をもう一度読んでみましょう
「以下の暗号文中の「彼」の名前を答えなさい」となっています
つまり暗号文中には「he」「his」「him」「name」などの単語が出てくることが容易に想像できます
これを踏まえると ?e→he(He) 、?i?→his(His)、?a?e→name になりそうだと想像できます
これを当てはめると
I ha?e a ????he?
His name is ???
He is an en?inee?
さらにha?e→have、en?inee?→engineerと予想できるので(hateなどはhaveほど頻出でないので)
I have a ?r??her
His name is ???
He is an engineer
となります
あとは文脈で判断します
上の文章は
私は「?r??her」を持っています。
彼の名前は「???」です。
彼はエンジニアです。
となって、一文目で「彼」に対応する単語が登場したと考えられます
そこで?r??her→brotherとしてみると
I have a brother.
His name is Bob.
He is an engineer.
となり、答えが「Bob(ボブ)」だと分かります。これで解読終了です
問題4(スキュタレー)
問題4:あなたは道端である細長い紙を見つけました。そこには縦書きで以下のように書かれていました
TEEDEHAIETESSRRTUUTERRNHE
この暗号を解読してください
これは古代ギリシャで戦争の際に用いられた暗号を改題したものです。
スキュタレーという円筒に細長い布を巻き付け、暗号化したい文章を横書きで書いて、円筒から外すことで、文字の順番が入れ替わった縦書きの暗号文を作ることができるというものです

今回出題した暗号は、全周に沿って5文字を、横方向に5文字を書き込める円筒を用いて暗号化しました
復号する際は4文字飛ばしで読めば良いので
T____H____E____T____R____
_E____A____S____U____R___
__E____I____S____U____N__
___D____E____R____T____H_
____E____T____R____E____E
となって元の文章は THE TREASURE IS UNDER THE TREE(宝は木の下にある)となります
何文字か飛ばして読めば良いと気づけば、あとは1文字飛ばし、2文字飛ばし、…と試して行けば良いので、どんな円筒を使ったか分からなくても復号は可能です