こんにちは、シンジです
前回に引き続き、論理パズルを紹介していこうと思います
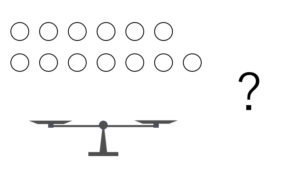
問題
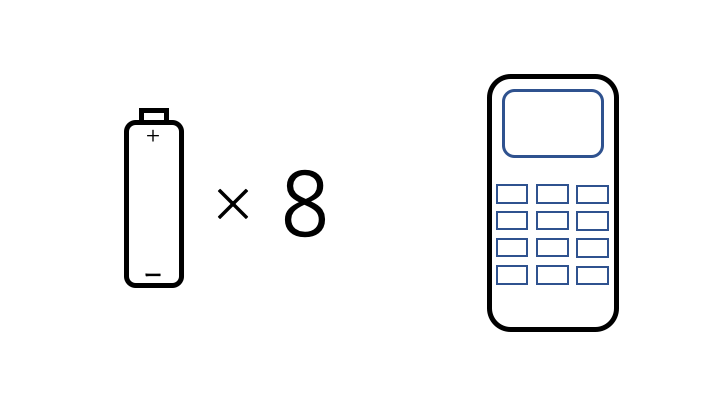
あなたは8本の乾電池と1つのリモコンを持っています。
リモコンを動かすには、使える乾電池が2本必要です
8本の乾電池のうち、4本は使える乾電池ですが、残りの4本はバッテリー切れで使うことができません
そこで、あなたは、実際にリモコンに2本ずつ挿して使える乾電池の組を探すことにしました。
7回以内に使える乾電池の組(2本)を確実に見つけ出し、リモコンを動かすにはどうしたらいいでしょうか
※「リモコンに2本挿す」という動作を1回と数えます。また、リモコンが動かなかった場合、2本とも取り外すことにします。ただし、確かめる際に電池の残量が減ることはないものとします。
解答
以下、解答です。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓解答↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
まず、8本の乾電池を3本、3本、2本の3グループに分け、順にAグループ、Bグループ、Cグループと名付けます。
次にAグループの3本の中に、使える乾電池の組が存在するか調べます
Aグループの3本の乾電池をA1, A2, A3 とすると、確かめるべき組み合わせは(A1, A2), (A2, A3), (A3, A1)の3通りです
もし3通り試してみてリモコンが動かなかったら、
「Aグループには使える乾電池が1本だけある」
「Aグループには使える乾電池が1本もない」
のいずれかということが分かります
次にBグループの3本についてAグループの時と同様に調べます
それでもリモコンが動かなかったら、AグループにもBグループにも1本しか使える乾電池がなかったことになるので、Cグループの2本をリモコンに挿して終了です
以上の方法を使えば、7回以内で確実にリモコンを動かすことができます