こんにちは、シンジです
今回はコインと天秤を使った論理パズルを紹介していこうと思います

問題
問題は以下の通り
13枚のコインがあります。この中に1つだけ重さの異なる偽物のコインが含まれています。
天秤をちょうど3回使って、偽物のコインを見つけ出してください。
ただし、偽物のコインが本物より軽いのか重いのかは分からないものとします。
また、偽物のコインが重いのか軽いのかは判別する必要はありません
「偽物のコインが本物より軽いのか重いのか」が分かっている場合には比較的簡単に解けるのですが、今回は分からないのでかなりの難問となっています
解答
以下、解答です。場合分けが多く煩雑なので、目次を使いながら読むことをおすすめします
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓解答↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
まず、コインを4枚、4枚、5枚に分け、順にAグループ、Bグループ、Cグループと名付けます

次に4枚のコイン2組(AグループとBグループ)を天秤に載せます(天秤の使用回数:1回目
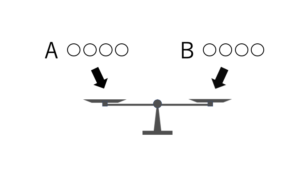
1回目で釣り合った場合
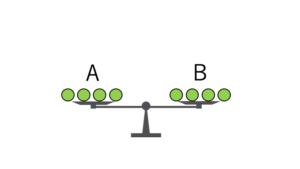
もし天秤が釣り合ったなら、天秤の上には本物のコイン(図の緑色)しかないことになるので、天秤に載せなかったコイン5枚(Cグループ)に偽物が含まれると分かります。
Cグループから偽物を見つけ出すために、今度は5枚のコインを3枚・2枚に分けます
分けた3枚、2枚のコインを順にC’グループ、C”グループと名付けます
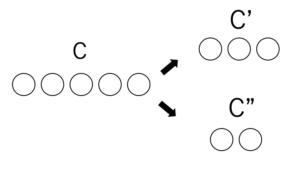
そして、分けた3枚のコイン(C’グループ)と、Aグループ(またはBグループ)の本物のコイン3枚を天秤にかけて重さを比べます(天秤の使用回数:2回目)
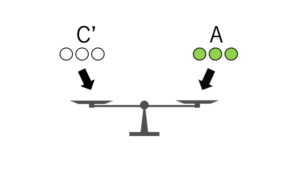
1回目も2回目の釣り合った場合
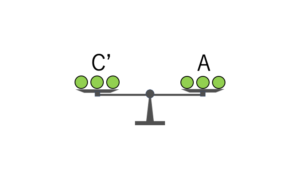
C’グループの3枚とAグループの3枚が釣り合ったなら、C’グループのコインは全て本物、すなわちC”グループの2枚のコインのどちらかが偽物だと分かります
そこで今度は、C”グループをのコイン1枚と、本物のコイン1枚を天秤にかけて(天秤の使用回数:3回目)、釣り合ったら天秤に載せなかった方のコインが偽物、釣り合わなかったら天秤に載せた方のコインが本物と分かります[終]
1回目で釣り合って、2回目で釣り合わなかった場合
C’グループの3枚とAグループの3枚が釣り合わなかったなら、C’グループの3枚のコインのどれかが偽物だと分かります
ここで
・C’グループが本物より重かった場合(C’グループの皿が下がった場合)と、
・C’グループが本物より軽かった場合(C’グループの皿が上がった場合)
に分けて考えます
●C’グループが本物より重かった場合
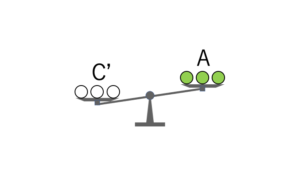
C’グループが本物より重かった場合には、C’グループに「本物より重い偽物」が含まれていることが分かります
よってC’グループの3枚のコインのうち2枚を天秤にかけた場合(天秤の使用回数:3回目)
・天秤が傾いたら、重い方が偽物
・天秤が釣り合ったら、載せなかったコインが偽物
だと分かります[終]
●C’グループが本物より軽かった場合
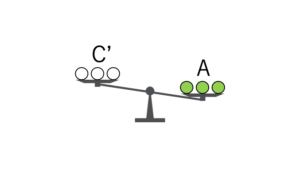
C’グループが本物より軽かった場合には、C’グループに「本物より軽い偽物」が含まれていることが分かります
よってC’グループの3枚のコインのうち2枚を天秤にかけた場合(天秤の使用回数:3回目)
・天秤が傾いたら、軽い方が偽物
・天秤が釣り合ったら、載せなかったコインが偽物
だと分かります[終]
1回目で釣り合わなかった場合
次に1回目で釣り合わなかった場合、すなわち
・Aグループの方が重かった場合(パターンA>B)
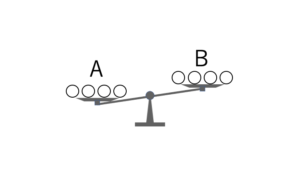
・Bグループの方が重かった場合(パターンA<B)
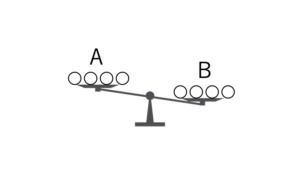
の2パターンについて考えていきます。
この場合、Aグループの4枚とBグループの4枚の計8枚の中に偽物のコインが含まれていることになります
ここで
・Aグループの4枚のコインをそれぞれ、A1,A2,A3,A4
・Bグループの4枚のコインをそれぞれ、B1,B2,B3,B4
と名付けることにします
そして、「A1,A2,B1」と「A3,A4,B2」を天秤にかけます(天秤の使用回数:2回目)
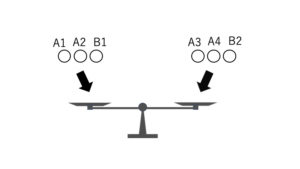
1回目で釣り合わなくて、2回目で釣り合った場合
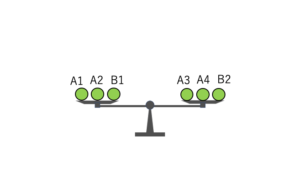
「A1,A2,B1」と「A3,A4,B2」を天秤にかけて、釣り合った場合、偽物は載せてない2つ (B3,B4)のどちらかになります
どちらが偽物か判別するためにB3,B4を天秤にかけます(天秤の使用回数:3回目)
ここで
・1回目の比較でAグループの方が重かった場合(パターンA>B)、B3,B4のどちかかが「本物より軽い偽物」
・1回目の比較でBグループの方が重かった場合(パターンA<B)、B3,B4のどちかかが「本物より重い偽物」
となるので
・パターンA>Bの時は、B3,B4のうち軽い方が偽物
・パターンA<Bの時は、B3,B4のうち重い方が偽物
と判別できます[終]
1回目も2回目の釣り合わなかった場合
1回目も2回目の釣り合わなかった場合
・「A1,A2,B1」の方が重い時(パターン1)
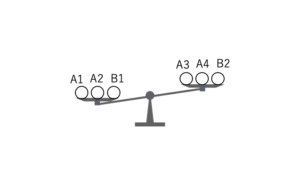
・「A3,A4,B2」の方が重い時(パターン2)
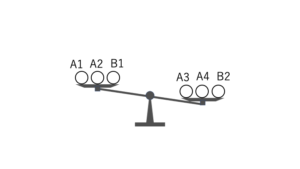
上の2通りについて考えていきます
●「パターンA>B」+「パターン1」
「パターンA>B」かつ「パターン1」の場合、以下の3通りの可能性が考えられます
・A1が「本物より重い偽物」
・A2が「本物より重い偽物」
・B2が「本物より軽い偽物」
これを踏まえて、A1とA2を天秤にかけ(天秤の使用回数:3回目)、その結果を考察すると以下のように偽物を見つけることができます[終]
・天秤が傾いたら、重い方が偽物
・天秤が釣り合ったら、B2が偽物
●「パターンA>B」+「パターン2」
「パターンA>B」+「パターン2」の場合、以下の3通りの可能性が考えられます
・A3が「本物より重い偽物」
・A4が「本物より重い偽物」
・B1が「本物より軽い偽物」
これを踏まえて、A3とA4を天秤にかけ(天秤の使用回数:3回目)、その結果を考察すると以下のように偽物を見つけることができます[終]
・天秤が傾いたら、重い方が偽物
・天秤が釣り合ったら、B1が偽物
●「パターンA<B」+「パターン1」
「パターンA<B」+「パターン1」の場合、以下の3通りの可能性が考えられます
・A3が「本物より軽い偽物」
・A4が「本物より軽い偽物」
・B1が「本物より重い偽物」
これを踏まえて、A3とA4を天秤にかけ(天秤の使用回数:3回目)、その結果を考察すると以下のように偽物を見つけることができます[終]
・天秤が傾いたら、軽い方が偽物
・天秤が釣り合ったら、B1が偽物
●「パターンA<B」+「パターン1」
「パターンA<B」+「パターン2」の場合、以下の3通りの可能性が考えられます
・A1が「本物より軽い偽物」
・A2が「本物より軽い偽物」
・B2が「本物より重い偽物」
これを踏まえて、A1とA2を天秤にかけ(天秤の使用回数:3回目)、その結果を考察すると以下のように偽物を見つけることができます[終]
・天秤が傾いたら、軽い方が偽物
・天秤が釣り合ったら、B2が偽物
これで全てのパターンについて天秤を3回だけ使って偽物を見つけ出すことができました
余談
天秤を使う回数がk回のとき、判別可能なコイン数の上限は、(3^k-1)/2で表されます(3^kは「3のk乗」)
コインがN枚ある時には可能性が2N通りあること(1枚目が軽い、1枚目が重い、2枚目が軽い、…、N枚目が重い)と
天秤を1回使うことで「右の方が軽い」「左右同じ重さ」「左の方が軽い」の3種類の情報が得られることから、判別可能なコイン数の上限が(3^k-1)/2になりそうだと予想できると思います
厳密な証明を知りたい人は以下のサイトを見ることをお勧めします
http://www-cr.scphys.kyoto-u.ac.jp/member/midori/HTML/kinka.html